This is an introduction about quantum computing, showing its supremacy and evolution. The idea of the article is to explain in a fast but conceptual way the potential of quantum computers.
Quantum physics is absolutely fascinating and wonderful, which deserves compression and understanding, because in the near future the future of computing will be quantum.
This article was written by a programmer and curious, for all programmers.
About the spicy thumps of two titans of physics: Einstein says: “God does not throw dice” and Bohr responds to Einstein “You should not tell God what to do”.
Quantum computing is an old topic, but it is now becoming possible to use it due to advances in research, driven by top techs such as Google, Intel, Microsoft and IBM.
Quantum computing is a technology that uses the properties of quantum mechanics to perform calculations at a significantly higher speed and with exponentially greater processing capacity than the classic computers we know today that use transistors.
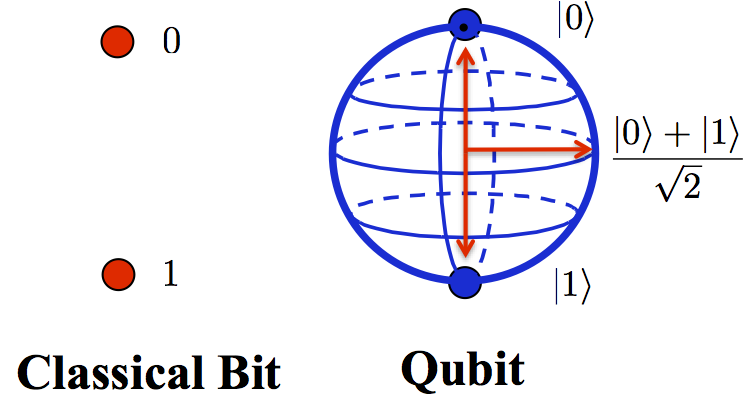
A classic computer uses individual (bits) that can contain a single state that we know as (0 or 1). Quantum computing merges this concept into a single bit, which is known as (qubit), a qubit can contain the value of (0 and 1) at the same time.
From the properties of quantum mechanics, dealing with (wave-particle duality). The quantum computer can perform calculations in a different and totally new way compared to the classic algorithms.
The potential of quantum computing is fantastic, there is enormous potential to apply this technology in a variety of software products such as database, search engines and extremely deep neural networks for intelligence artificial.
In this article we will address a little history of quantum mechanics because this understanding is necessary and because it becomes different from classical physics. And finally in the next article we can create in the quantum programs to analyze.
Who is an academic or studying physics, knows the discussions between Einstein and Bohr on the subjects of quantum mechanics. The idea does not enter into this clash but it is interesting to be studied. Einstein says, “God does not throw dice” and Bohr tells Einstein “You should not tell God what to do”.
But we know that before quantum physics was discovered, they were all very comfortable with the explanations of classical physics. The fact is that classic physics does a good job in explaining the macroscope world, the world we can see, feel and touch, the world that contains massive particles, however as you move through the world macroscope things start to behave in a way different.
In the macroscope world we can see and touch things, pick up the mace and throw it on the ground, you know it will fall, roll and stop. Certainly she did not want to run to the center of the earth. But when we enter the microscope world, quantum physics emerges and we realize that these properties may be quite different.
In quantum physics, the concept of pixelation is used, within the microscopic world, the physical quantities do not move more smoothly from one state to another, instead they become pixelated, that is, as if the image were blurred.
In quantum physics, an object can appear in several places simultaneously simultaneously. This is due to the effects of probability at the microscopic level, which allows the electron or a photon to be present in different places at the same time.
Another quantum physics challenge is a lot of uncertainty when dealing with the microscope world. In classical physics we have an accurate measurement, a location, and a known velocity. In the microscopic world the results are based on probability with a degree of error. This uncertainty occurs because it is necessary to measure the position of the particle, and to measure this particle in the case an electron is required that light is in the form of photon. Therefore we can not know where and how fast the object is moving, because the moment we observe it, it changes.
With this little introduction of quantum physics and classical physics, let’s look at how quantum physics is being used in computing.
The double-slit experiment demonstrates the unique property of the wave-particle duality that exists in the quantum world. This is the key behavior that leads to the properties of quantum computing.
Watch a visual video explaining the double-slit experiment:
As we can see there are several differences between classical and quantum computers. These factors include the amount that can be processed in single computation cycle as well as processing speed of information.
The classic computers we use today, at home in the work office, rely on transistors. A transistor has a “high” voltage measurement, the value of (bit) is considered 1. Similarly, when the transistor has a “low” measurement, the value considered is 0. Inside a CPU chip thousands of small transistors, for example a CPU (Intel Core i7 Quad) has 731,000,000 transistors, one (IBM Power8 12 core) has 4,200,000,000 transistors.
As electricity is flowing through the wires and gates, it is limited by the speed that moves through the wires moreover, the transistor can only represent the value (0 or 1) on or off, ie (high) or (low), but never at the same time.
Thus a classical computer can represent a bit of information with value (0 or 1) and this is expressed in operation (XOR), so a classical computer can process (n bits) in a single CPU cycle.
Quantum computers have a completely different technology to represent one (bit) information. Quantum computing takes advantage of quantum physical properties to perform calculations. A quantum computer does not use transistors, instead it uses electrons and photons that are measured according to their quantum properties, the result is (0 or 1) or a probability between them. Because of the unique properties of this particle at the microscopic level, they can hold a value (0 or 1) and simultaneously be measured. This quantum mechanical property is known in quantum computation as (superposition).
The representation of a single (bit) in quantum computation is called (qubit). Think about what that means in quantum computer processing power. Notice in the image below the comparison of one (bit and qubit).

Therefore a single (bit) can hold a value (0 or 1), while a (qubit) can contain (2 bits) of information (0 and 1). Similarly a (2 qubits) may contain (4 bits) of information (00, 01, 10, 11). We go further we can see that (3 qubits) give us 8 states, 4 give us 16.5 give us 32 and so on. In this way a quantum computer can process (2 ^ n bits) information simultaneously per computing cycle.
Watch the video on (qubit) at:
If we think of an exponential representation in the processing power of the quantum computer and classical computer, we can extrapolate the number of (qubits), a quantum computer of 50 (qubits) can process (2 ^ 50 bits) information in a single cycle, or (1e + 15 bits) of information, compared to a classical computer that could simply process (50 bits) of information with the same number of transistors.
When we measure exponentially, the single-cycle processing capacity of a quantum computer becomes clear. Let’s see what this means in data processing.
Now that we know the exponential processing power of a quantum computer. Let’s check how it’s built:
Companies like Google, IBM, and Intel already own their quantum computers. IBM for example has the (IBM Q) it uses superconducting loops where electricity can flow without loss. An electric current oscillates back and forth within the circuit, where the microwaves can be used to excite the state of electrons (qubits) to perform operations. To stabilize the electrons and isolate them from external interference it is necessary that the quantum computer is at a temperature of (0.015) Kelvin in degrees Celsius (-273).
A quick comparison of temperatures in different regions of the universe:
| Location | Kelvin | Celsius |
|---|---|---|
| Qubit | 0.015 | -273 |
| Vacuum of the space | 2.7 | -270 |
| Average temperature of Earth | 331 | 58 |
| Temperature of the moon at daytime and night | 373/100 | 100/-173 |
In addition, it is necessary to interact with the (qubits) and translate them in a way already used in classic computers. This is done using a classical computer process, where the quantum computer receives an input where the information is processed using a quantum computational algorithm. The result of the processing is then passed to a classic computer that interprets the data and sends the output to the user.
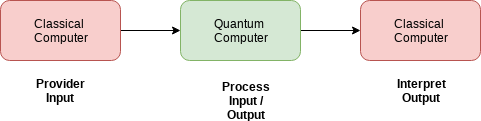
So the precise quantum computer lies between two processes of a classic computer, one for data entry and another for data output.
We already understand with the quantico computer works, we have seen the properties of quantum physics, and we also understand the concept of superposition.
But quantum mechanics can be even more mysterious. Besides the behavior of electrons in waves and particles, there is also the concept of (quantum interlacing). One (qubit) can interact with others (qubits) in the same state, this is called (entanglement). One (qubit) can not be measured without measuring all (entangled qubits). In addition, this (entanglement) can occur in large separation distances, one (qubit) can influence another (qubit) that is physically distant.
Einstein called this phenomenon (phantasmagoric action at a distance). This is because two electrons may be physically distant, and if one is measured or modified the other would assume the same value. This point is still a matter of study and exploration for scientists.
Within the quantum system, a wave function can describe a behavior, velocity or motion of the particle. As long as the particle is in the overlapping state its function of where it exists and is valid. However when measuring the particle’s value, this single action causes a collapse in the wave function. This collapse results in (0 or 1) and no more the two simultaneous and the wave function is reduced.
Remember that when one electron (interlaced) is measured, the other electron will maintain a corresponding value regardless of the distance between them.
There are still other theories for (interlacing) which are (multiple universes), (the invisible force), and (in free will), but we will not address those topics here.
There are a range of applications that quantum computers will help:
One of the main targets of quantum computing is Big Data. The amount of data will increase even more, and we need to process that information to generate intelligence even more quickly. Let’s consider an example of Facebook.
We can calculate the Big Data in (peta-bytes), this is because it is not very large. A peta-byte equals (10 ^ 15) bytes. We want to compare this with (qubits) which are described by (2 ^ q) rather than (10 ^ 15) say (2 ^ 50 bytes), because the values are similar. This means that a quantum computer can process (1 peta-byte) of information in only a single calculation cycle.
If Facebook chooses to store data of 2 billion accounts, this can represent the magnitude of (500 peta-bytes). A quantum computer with (60 qubits) can process this information in only a single calculation cycle.
This is just an example of use, we can think of quantum computing for cryptography and a number of algorithms that today are extremely costly to process them.
Aviation and aerospace companies in general can benefit from quantum applications. For example the use of quantum algorithms for simulations, missions. Applications that require artificial intelligence algorithms.
The medical industry can benefit by using applications for molecular simulation, drug testing, DNA analysis, and models that are still complex and slow for classic computers today.
The next step in this article is to install and configure our environment to create our first quantum program.
Documents that helped in the publication of this article:
Thanks!